Площадь равнобедренного треугольника
Формула площади равнобедренного треугольника
- по основанию и высоте
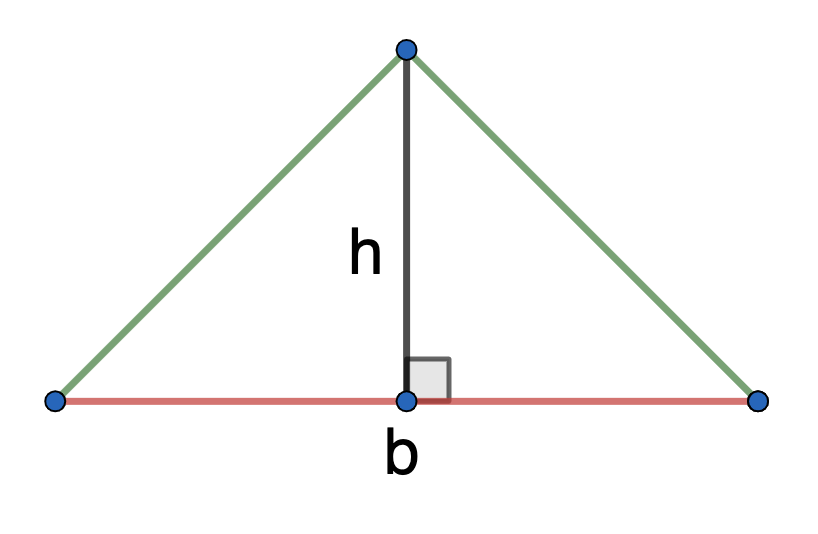
\(S_\bigtriangleup = \frac{1}{2} b*h\)
\(b\) - основание
\(h\) - высота
- по двум сторонам
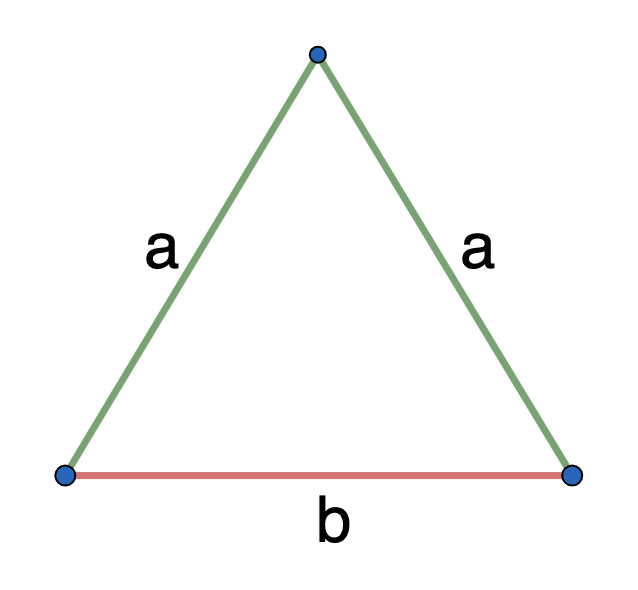
\(S_\bigtriangleup = \frac{b}{4} \sqrt{ 4a^2-b^2}\)
\(b\) - основание
\(a\) - стороны
\(h\) - высота
- если в равнобедренном треугольнике прямой угол
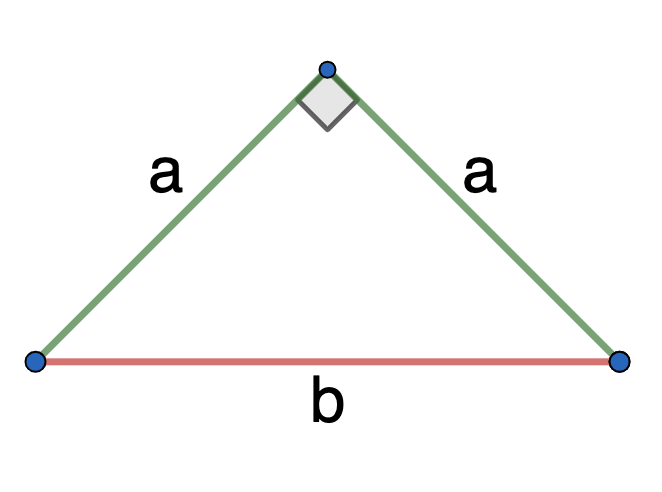
\(S_\bigtriangleup = \frac{1}{2} a^2\)
\(a\) - равные стороны, между которыми 90°
Примеры
Найдите площадь равнобедренного треугольника, если боковая сторона равна 10, а основание 12.
Решение: Воспользуемся формулой подсчета по двум сторонам \(S_\bigtriangleup = \frac{b}{4} \sqrt{ 4a^2-b^2} = \frac{10}{4} \sqrt{ 4*12^2-10^2} = 54,5\)
Как найти площадь равнобедренного треугольника, зная, что основание равно 30, а высота, проведенная к основанию - 12.
Используем формулу \(S_\bigtriangleup = \frac{1}{2} b*h = \frac{1}{2} 30*12 = 180\) . Ответ 180.
Чему равно основание равнобедренного треугольника, если нам известно, что его площадь равна 180, а высота, проведенная к основанию равна 30.
Решение: Используем первую формулу, из нее следует что \(b = \frac{S*2}{h} = 180*2/30 = 12\)
b - основание
S - площадь треугольника
h - высота

