Площадь прямоугольного треугольника
Основные определения
Прямоугольный треугольник - это такой треугольник, в котором один из углов равен 90° (прямой угол).
Катеты - стороны, прилежащие к прямому углу 90°.
Гипотенуза - сторона, противолежащая прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно воспользоваться несколькими формулами.
Формула площади прямоугольного треугольника через катеты
\(S = {{a*b} \over 2}\)
a, b - катеты
Формула площади прямоугольного треугольника через гипотенузу
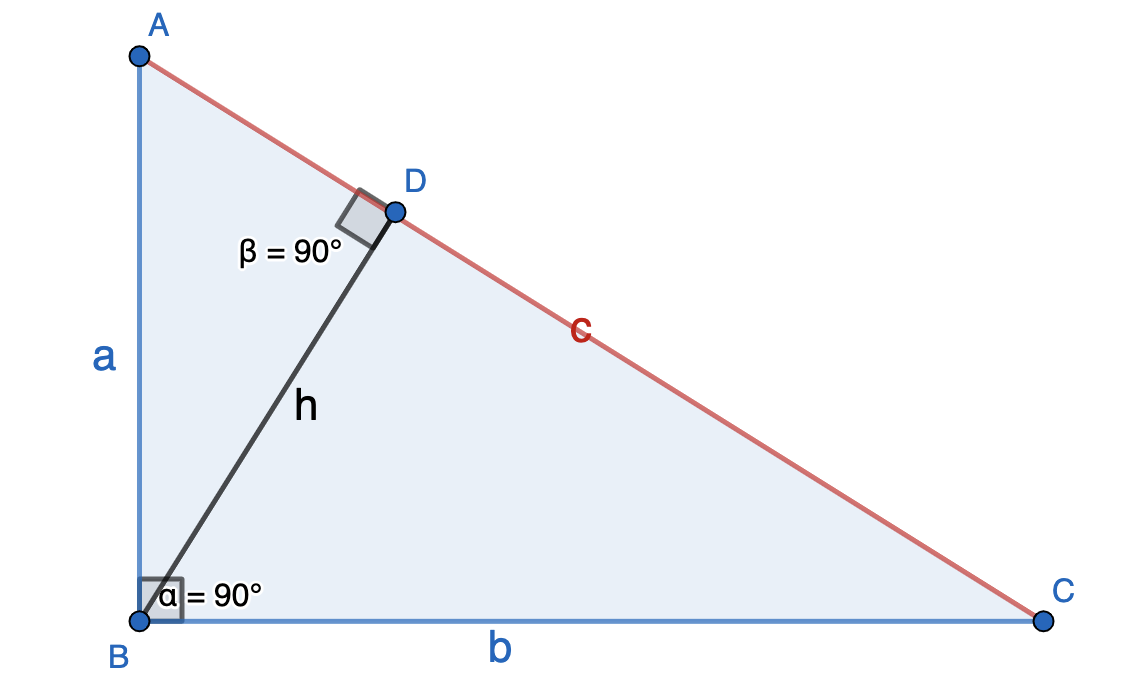
\(S =1/2(c*h)\)
\(c\) - длина гипотенузы,
\(h\) - высота.
В прямоугольном треугольнике высота находится по формуле:
\(h = \frac{a*b}{c}\)
\(a\) - длина одного катета,
\(b\) - длина второго катета.
Формула площади прямоугольного треугольника через острый угол и гипотенузу
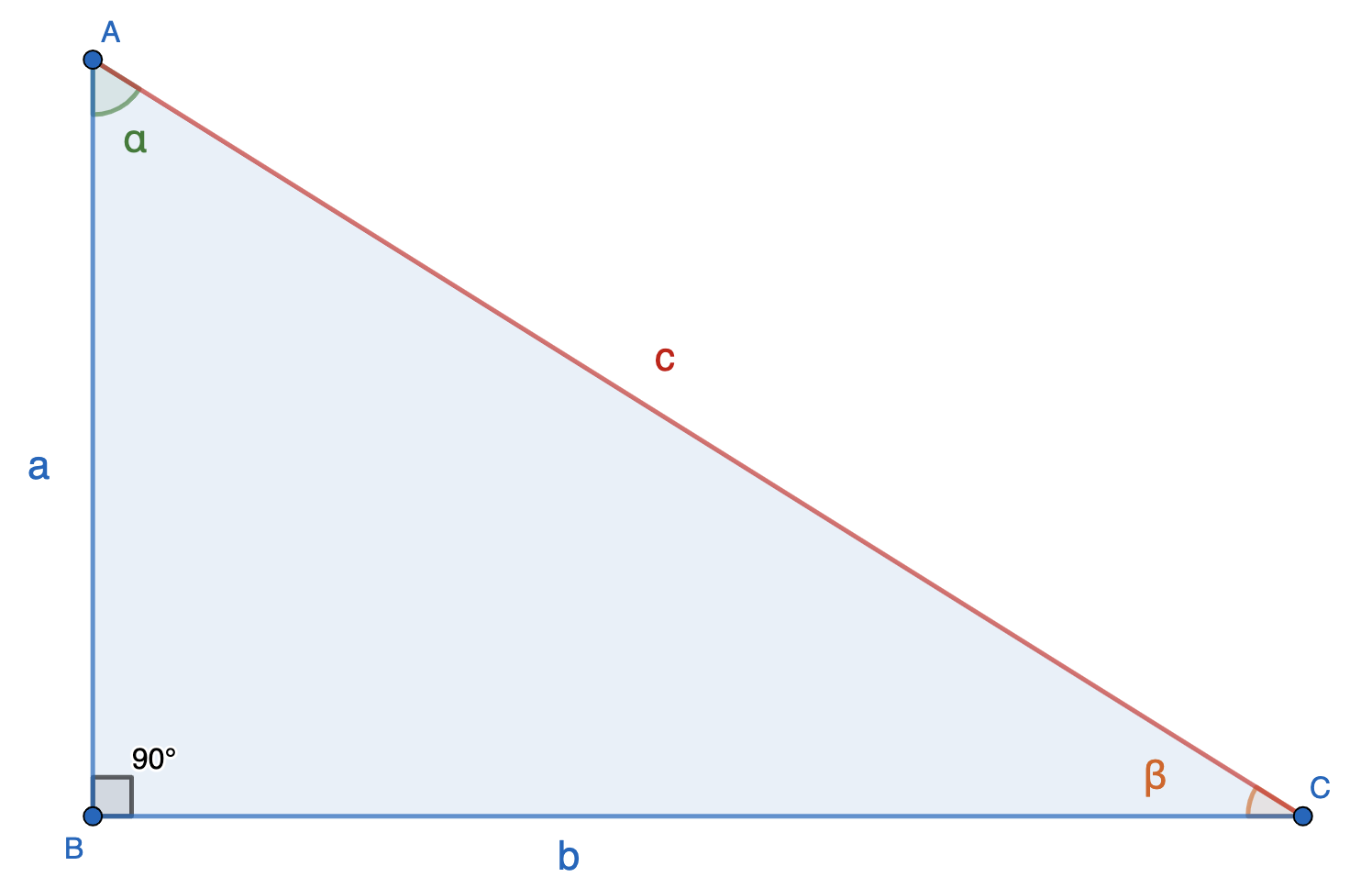
Если известны острый угол и гипотенуза, то посчитать площадь можно так:
\(S = \frac{c^2*sin\alpha*cos\alpha}{2}= \frac{c^2*sin(2\alpha)}{4}\)
\(S = \frac{c^2*sin\beta*cos\beta}{2}= \frac{c^2*sin(2\beta)}{4}\)
\(c\) - гипотенуза
\(\alpha\) и \(\beta\) - острые углы
Формула площади прямоугольного треугольника через катет и острый угол
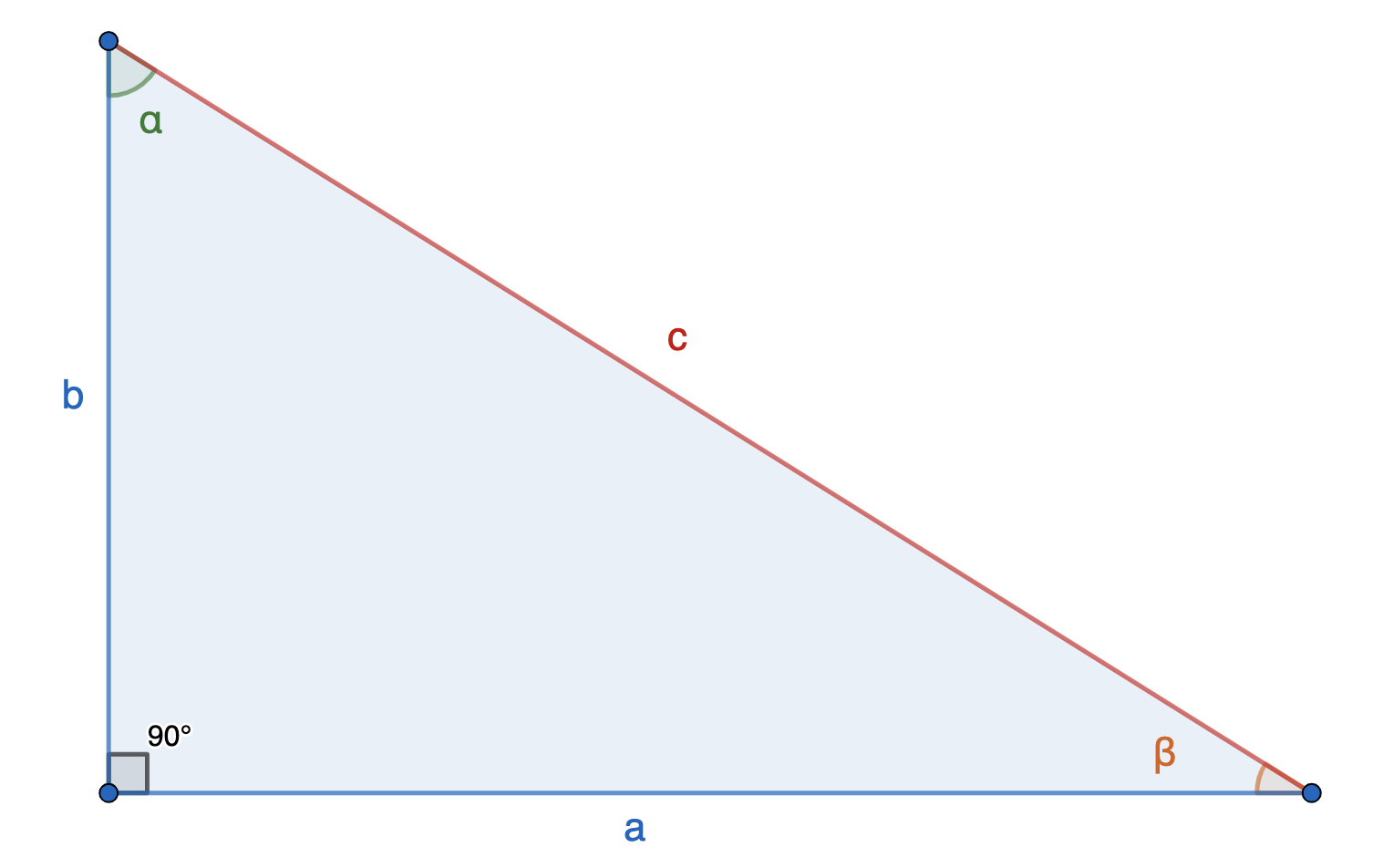
Если известен один катет и острый угол, то рассчитываем площадь так:
\(S = {{a^2*tg\beta} \over 2}\)
\(S = {{b^2*tg\alpha} \over 2}\)
\(a\), \(b\) - катеты
Формула площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
\(S = r (r+c)\)
\(r\) - радиус вписанной окружности
\(с\) - гипотенуза