Площадь прямой призмы с основанием ромб
Пример 1:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями 4 и 10, и боковым ребром равным 12.
Решение:
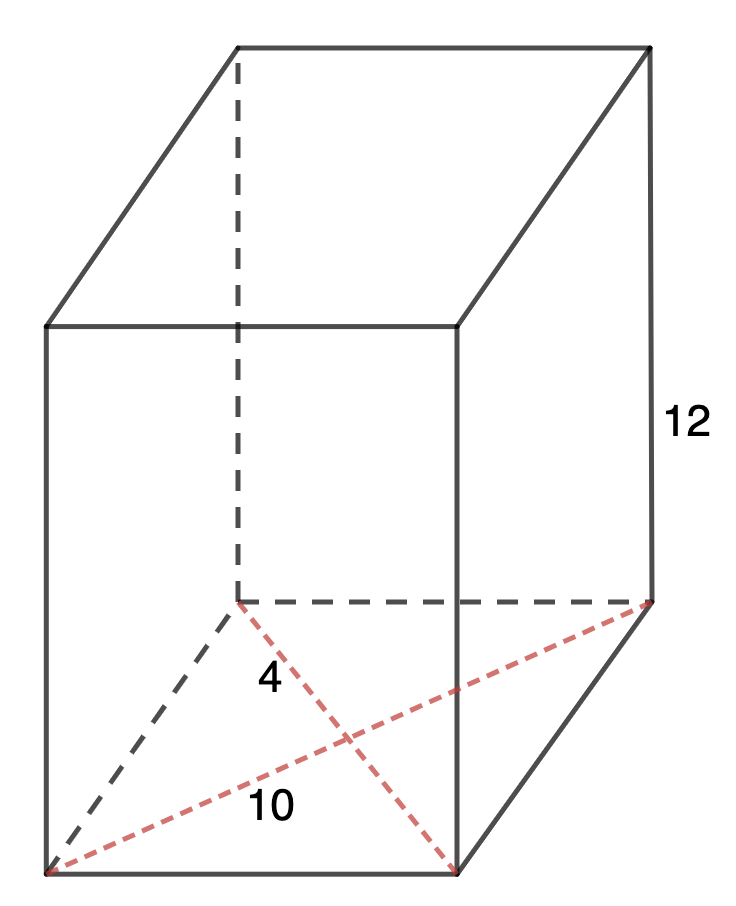
Чтобы найти полную площадь поверхности, нужно сложить четыре площади боковых поверхностей и две площади оснований (ромба).
Площадь ромба найдем по формуле:
\(S_{основания} = \frac{1}{2}*d1*d2 = \frac{4*10}{2} = 20\)
Для нахождения площади боковых граней нужно найти грань основания.
Длина грани ромба = \(\sqrt{4^2+10^2} = \sqrt{116} = 10.77\), где 4 и 10 - диагонали ромба из условия задачи.
\(S_{бок} = 4*(12*10,77) = 516,96\)
\(S_{полн} = S_{бок}+2*S_{осн} = 516,96+2*20 = 556,96\)
Ответ: 556,96.

